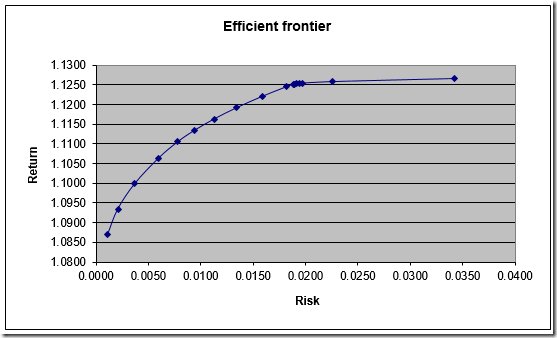
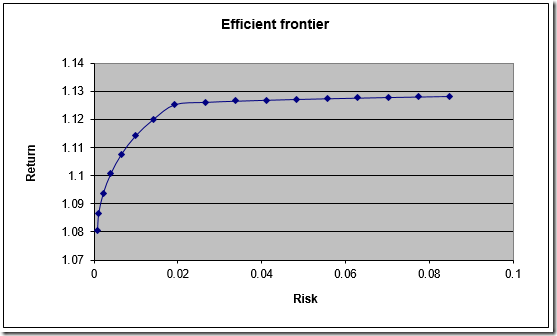
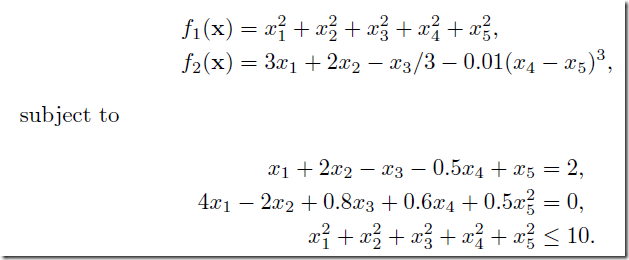When tracing an efficient frontier sometimes the pictures indicate that points are not very evenly distributed:
In the paper http://www.sciencedirect.com/science/article/pii/S0895717710006424
an interesting algorithm is developed to trace the Pareto frontier with points that are nicely spread out. The idea is to find the next point by adding a distance constraint to problem. The next point should be a fixed distance from the previous point. Lets try one of the examples in the paper.
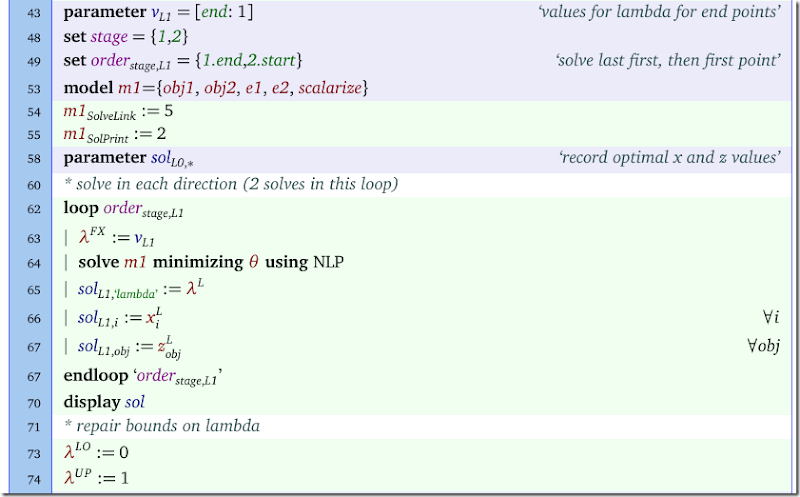
The declarations are:
Note that the weight λ is now a (nonlinear) variable.
The example
is implemented as:
The first step is to evaluate the points related to λ=0 and λ=1. I.e. optimize for each objective individually. (In my experience it is sometimes better not to have the “other” objective just float, but rather have a small weight on that objective. I.e. use λ=0.001 and λ=0.999.)
In line 43, the value for start we keep at zero (which is the default in GAMS). In the above loop we made sure to work on obj2 (λ=1) first and on obj1 (λ=0) second. This is to make sure the last point is a good starting point for the loop over the interior points we will do later.
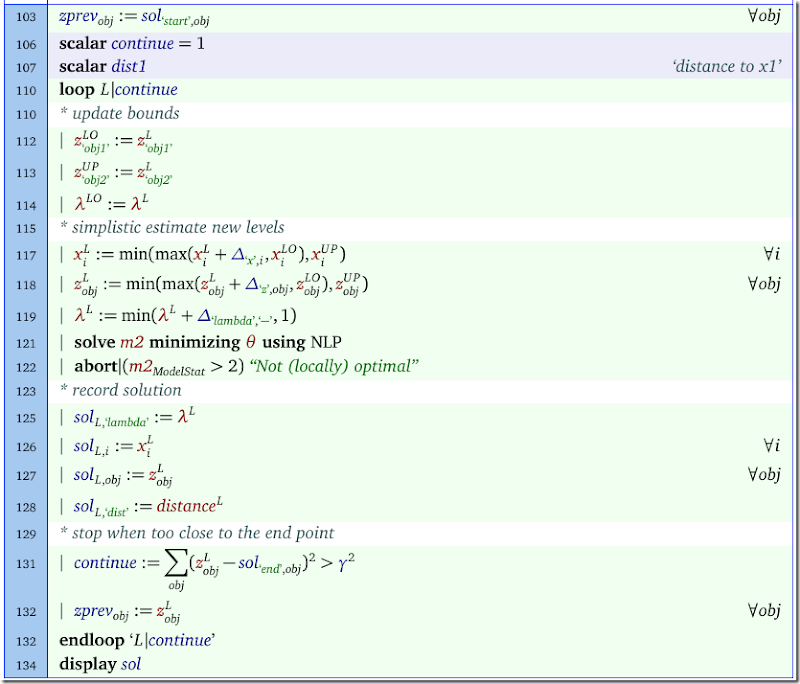
Next we calculate the distance between two points γ2. We also introduce a constraint that forces the distance between a new point and the last point is γ2. I would conjecture that a normalized distance would be more appropriate of the different objectives have different units.
The parameter Δ is used as a simple way to predict a step.
Finally we can execute the main loop:
We set some bounds on the objective variables z (and λ) so we don’t make a step backwards. We estimate the new point using an extremely simple interpolation mechanism. This method is in general not providing a feasible initial solution for the next point. In the paper it is mentioned they use a smarter estimate that is always feasible. I don’t see immediately how to generate such a starting point.
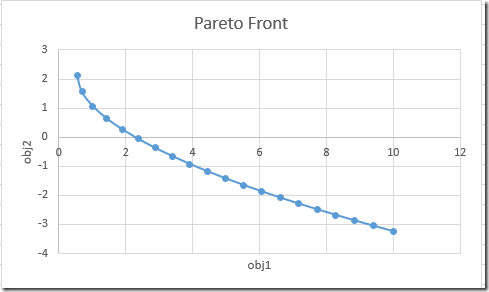
For the example in question, we get the following picture:
Finally, we can improve on our first picture: