In http://yetanothermathprogrammingconsultant.blogspot.com/2015/09/linearizations.html an example of a 2-objective land allocation problem is discussed. There are two competing objectives:
- Cost: assign plots such that total development cost is minimal.
- Compactness: cluster plots with the same land-use category together.
A pure cost based solution can look like the left picture below. When we take into account the compactness objective we could see something like the right picture.
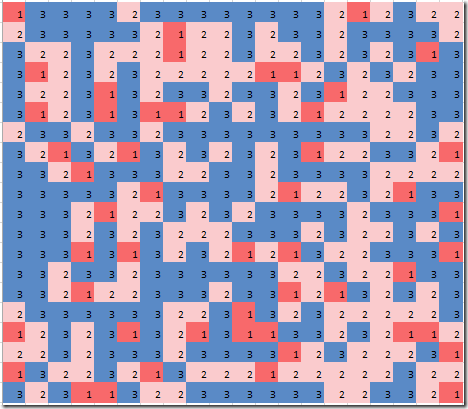 |  |
| Minimize Cost only | Minimize cost-α*compactness |
These “plots” were just colored cells in an Excel spreadsheet. Now a more interesting and dynamic plot can be made if we play with the trade-off α between cost and compactness. That is done in the plot below. This was done using R and the packages ggplot2 and animation.
Notes:
- If you pay careful attention you will notice that the dynamic plot and the static excel graphs have the y-axis reversed.
- It may be a good idea to apply some compactness constraints on political districts (in the US). This would reduce some of the crazy maps that are the result of gerrymandering. Compactness still can lead to unfair results, see: https://www.washingtonpost.com/news/wonk/wp/2015/03/01/this-is-the-best-explanation-of-gerrymandering-you-will-ever-see/.
- The above dynamic gif was the result of solving 50 MIP models.
