In [1] a simple optimization problem is posted:
My geometry is a bit rusty, but the necessary formulas can be found in [2]. The recap, the squared distance \(d^2\) between a point \(q\) and a single line through \(p_a\) and \(p_b\) is given by:\[d^2=\frac{|p_a-q|^2 |p_b-p_a|^2 - \left[(p_a-q)\cdot (p_b-p_a) \right]^2}{|p_b-p_a|^2}\] where \(\cdot\) indicates the dot product.
Actually just finding the shortest distance between a given line and a given point can be interpreted as an optimization problem:
We have multiple lines and the position of the point is not given. An optimization model to find the best place for our point \(q\) can be formulated as:
\[\min_q\>\sum_j \frac{|p_{j,a}-q|^2 |p_{j,b}-p_{j,a}|^2 - \left[(p_{j,a}-q)\cdot (p_{j,b}-p_{j,a}) \right]^2}{|p_{j,b}-p_{j,a}|^2}\] This thing is convex, so it is somewhat easy to solve as a QP (Quadratic Programming) problem.
Actually I cheated a bit: I minimized the sum of the squared distances. When really minimizing the sum of the distances we need to minimize: \[\min_q\>\sum_j \sqrt{\frac{|p_{j,a}-q|^2 |p_{j,b}-p_{j,a}|^2 - \left[(p_{j,a}-q)\cdot (p_{j,b}-p_{j,a}) \right]^2}{|p_{j,b}-p_{j,a}|^2}}\] This can be solved as an NLP (Nonlinear Programming) model.
How do results compare? For a 3D problem with 10 random lines I see:
Here the \(x,y,z\) values are the coordinates of \(q\). The column marked obj indicates the objective function value. In our 2D example we can see the differences more clearly:
The differences are a little bit more pronounced than I would have predicted.
A 3d visualization would be interesting.
Find a single point \(q\) in 3d space that is closest to a number of given lines. Each line \(L_j\) is defined by two points \(p_{j,a}\) and \(p_{j,b}\).
My geometry is a bit rusty, but the necessary formulas can be found in [2]. The recap, the squared distance \(d^2\) between a point \(q\) and a single line through \(p_a\) and \(p_b\) is given by:\[d^2=\frac{|p_a-q|^2 |p_b-p_a|^2 - \left[(p_a-q)\cdot (p_b-p_a) \right]^2}{|p_b-p_a|^2}\] where \(\cdot\) indicates the dot product.
Actually just finding the shortest distance between a given line and a given point can be interpreted as an optimization problem:
| Shortest distance between a line and a point |
We have multiple lines and the position of the point is not given. An optimization model to find the best place for our point \(q\) can be formulated as:
\[\min_q\>\sum_j \frac{|p_{j,a}-q|^2 |p_{j,b}-p_{j,a}|^2 - \left[(p_{j,a}-q)\cdot (p_{j,b}-p_{j,a}) \right]^2}{|p_{j,b}-p_{j,a}|^2}\] This thing is convex, so it is somewhat easy to solve as a QP (Quadratic Programming) problem.
 |
| 2D example: Minimize sum of squared distances |
Actually I cheated a bit: I minimized the sum of the squared distances. When really minimizing the sum of the distances we need to minimize: \[\min_q\>\sum_j \sqrt{\frac{|p_{j,a}-q|^2 |p_{j,b}-p_{j,a}|^2 - \left[(p_{j,a}-q)\cdot (p_{j,b}-p_{j,a}) \right]^2}{|p_{j,b}-p_{j,a}|^2}}\] This can be solved as an NLP (Nonlinear Programming) model.
How do results compare? For a 3D problem with 10 random lines I see:
---- 54 PARAMETER results
x y z obj
squared dist 0.015 -0.069 -0.2824.087
dist 0.050 -0.142 -0.4135.634
Here the \(x,y,z\) values are the coordinates of \(q\). The column marked obj indicates the objective function value. In our 2D example we can see the differences more clearly:
 |
| Added blue point: Minimization of sum of distances |
The differences are a little bit more pronounced than I would have predicted.
Minimax Model
A different objective can be formed by minimizing the maximum distance:\[\begin{align} \min\> & z\\ &z \ge d_i\end{align}\] We get the same solution if we minimize the maximum of the squared distance: \[\begin{align} \min\> & z\\ &z \ge d^2_i\end{align}\] This means we have a convex quadratic model. This will shift our location to the right:
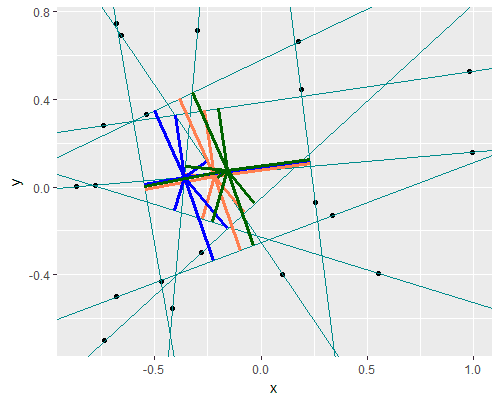 |
| Added green point: Minimize maximum of distances |
A 3d visualization would be interesting.
References
- Non-linear Optimization about Point to Lines, https://stackoverflow.com/questions/49594754/non-linear-optimization-about-point-to-lines
- Eric Weisstein, Point-Line Distance -- 3 Dimensional, http://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html