Inverting a large, dense matrix

In this post I show some experiences with inverting a large, dense matrix. The variability in performance was a bit surprising to me.

Background

I have available in a GAMS GDX file a large matrix \(A\). This is an input-output matrix. The goal is to find the so-called Leontief inverse \[(I-A)^{-1}\] and return this in a GAMS GDX for subsequent use [1]. It is well-known that instead of calculating the inverse it is better to form an LU factorization of \(I-A\) and then use that for different rhs vectors \(b\) (essentially a pair of easy triangular solves). [2] However, economists are very much used to having access to an explicit inverse.

A GAMS representation of the problem can look like:

set
r 'regions'/r1*r2/
p 'products'/p1*p3/
rp(r,p)
;

rp(r,p) = yes;

table A(r,p,r,p)

        r1.p1 r1.p2 r1.p3 r2.p1 r2.p2 r2.p3
r1.p1    0.8    0.1
r1.p2    0.1    0.8    0.1
r1.p3           0.1    0.8    0.1
r2.p1                  0.1    0.8    0.1
r2.p2                                0.8    0.2
r2.p3                  0.1    0.1    0.1    0.7

;

parameters
   I(r,p,r,p)   'Identity matrix'
   IA(r,p,r,p)   'I-A'
;
alias(rp,rp2,rp3);
I(rp,rp) = 1;
IA(rp,rp2) = I(rp,rp2) - A(rp,rp2);
option I:1:2:2,IA:1:2:2;
display I,IA;

*-------------------------------------------------------------------
* inverse in GAMS
*-------------------------------------------------------------------

variable
   invIA(r,p,r,p)   'inv(I-A) calculated by a CNS model'
;

equation LinEq(r,p,r,p)   'IA*invIA=I';

LinEq(rp,rp2).. sum(rp3, IA(rp,rp3)*invIA(rp3,rp2)) =e= I(rp,rp2);

model Linear /linEq/;
solve linear using cns;

option invIA:3:2:2;
display invIA.l;

* accuracy check.
* same test as in tool
scalar err 'max error in | (I-A)*inv(I-A) - I |';
err = smax((rp,rp2),abs(sum(rp3, IA(rp,rp3)*invIA.l(rp3,rp2)) - I(rp,rp2)));
display err;

The problem at hand has a 4-dimensional matrix \(A\) (with both regions and sectors as rows and columns). Of course, the real problem is very large.

Attempt 1: Microsoft Visual C++ with the Eigen library.

Here I use the Micosoft Visual C++ compiler, with the Eigen [3] library. Eigen is a C++ template library. It is very easy to use (it is a header only library). And it provides some interesting features:

It contains quite a few linear algebra algorithms, including LU factorization, solving, and inverting matrices.
It allows to write easy-to-read matrix expressions. E.g. to check if things are ok, I added a simple-minded accuracy check: \[\max | (I-A)^{-1} \cdot (I-A) - I | \] should be small. Here \(|.|\) indicates elementwise absolute values. This can be written as:
double maxvalue = (INV * IA - MatrixXd::Identity(matrixSize, matrixSize)).array().abs().maxCoeff();
Support for parallel computing using OpenMP [4]. MSVC++ also supports this.

The results are:

Notes:

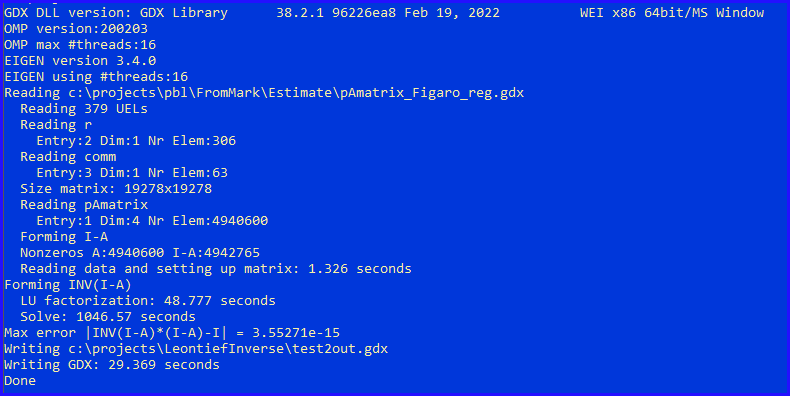
By default OMP (and Eigen) uses 16 threads. This machine has 8 cores and 16 hardware threads.
Reading the input GDX file is quite fast: 1.3 seconds. (Note: this is read in "raw" mode for performance reasons). There is also some hashing going on.
The nonzero count of \(I-A\) is 4.9 million. The inverse will be dense, so \(19278^2=372\) million elements. We use here dense storage schemes and dense algorithms.
Instead of calling inverse(), I split the calculation explicitly into two parts: LU decomposition and solve. The time to perform the LU factorization looks reasonable to me, but the solve time is rather large.
We can write the GDX file a bit faster by using compression. The writing time goes down from 29.4 to 14.8 seconds.

Why is the solve so slow? The following pictures may show the reason:

CPU usage during LU decomposition

CPU usage during solve

Basically, during the solve phase, we only keep about 2 cores at work. I would expect that multiple rhs vectors (and a lot of them!) would give more opportunity for parallelization. I have seen remarks that this operation is memory bound, so adding more threads does not really help.

Attempt 2: Intel/Clang with the MKL library.

Here I changed my toolset to Intel's Clang compiler icx, and its optimized MKL library. The Clang compiler is part of the LLVM project, and is known for excellent code generation. The MKL library is a highly optimized and tuned version of the well-known LAPACK and BLAS libraries. It is possible to use MKL as a back-end for Eigen, but here I just coded against MKL directly (I just have one LU decomposition, an invert, and a matrix-multiplication in the check). So how does this look like?

CPU Usage during solve

This looks much better.

Notes:

MKL only uses 8 threads by default: the number of physical cores.
Both the LU decomposition, but especially the solve part is much faster.
Here we used compression when writing the GDX file.
I used Row Major Order memory layout (i.e. C style row-wise storage).
MKL is a bit more low-level. Basically, we use LAPACK and BLAS calls.

Conclusion

Intel/Clang/MKL can be much faster than MSVC/Eigen on some linear algebra operations. The total time to invert this matrix went from > 1000 seconds to 100 seconds: